Mannigfaltigkeiten
Table of Contents
Mannigfaltigkeiten - Motivation #
Momentan beschäftige ich mich mit differenzierbaren Mannigfaltigkeiten. Das Interesse dieses interessante mathematische Konzept verstehen zu wollen, ist zu groß, als nicht einen Versuch dahingehend zu unternehmen. Dieser Eintrag und kommende unterliegen der Vorsicht, die bei diesem Thema zu walten hat, und sind daher unter ständiger Überarbeitung. ;)
Ich habe mir das Buch von Manfredo Perdigão Do Carmo - Riemannin Geometry als Hilfslektüre vorgenommen und werde von dort aufbauend das Thema angehen.
Einleitung #
Um allgemein einen Eindruck einer differenzierbaren Mannigfaltigkeit zu erhaschen, stelle ich hier kurz das Algebra-Konzept vor:
- Zunächst einmal gehen wir von einer Allgemeinen Oberflächen in \(R^{3}\) aus.
- Wir sagen weiter, dass eine Oberfläche im Raum \(R^{3}\) eine Teilmenge von \(R^{3}\) ist, also \(S \subset R^{3}\) .
- Weiterhin existiert für jeden Punkt \(p \in S\) eine Nachbarschaft \(V\) die an \(p\) in \(R^{3}\) liegt (das ist hier zunächst abstrakt gemeint, stell dir einfach vor, dass \(p\) dadurch irgendeine Umgebung hat).
- Die Zuordnung von einer offenen Menge \(U \subset R^{2}\) über \(\mathbf{x}:U \subset R^{2} \rightarrow V \cap S\) erreicht eine Nachbarschaft, welche eine Schnittmenge mit \(S\) hat. Die Gestaltung dieser Zuordnung ist in ihrer Art so, dass:
- \(\mathbf{x}\) eine differenzierbare Abbildung ist. Das bedeutet, dass wir annehmen, dass sich die Nachbarschaft \(V\) nicht groß von \(U\) unterscheidet. Sie unterscheidet sich nur infinitesimal. Der einfachste Fall dieses Verhältnisses lässt sich über die Berechnung der Steigung, also die Differenz zwischen zwei zueinander definierten Punkten aufzeigen. In folgender Grafik ist der \(dx\)-Differential-Quotient dargestellt.
Der Differential-Quotient #
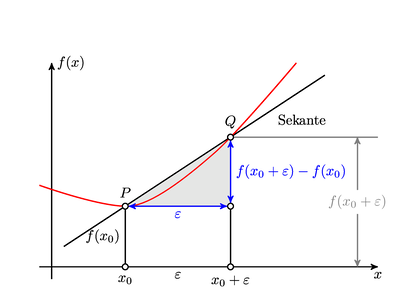
Eine ähnliche Darstellung im 3-dimensionalen lässt sich auch finden:
- Und das Differential \(d\mathbf{x}_{q}:R^{2} \rightarrow R^{3}\) injektiv für alle \(q \in U\) ist.
Wir können zu der Zuordnung \(\mathbf{x}\) auch sagen, dass dies eine Parametrisierung von \(S\) durch \(p\) sei. Nimmt man nun an, dass im einzelnen mehrere Zuordnungen o.g. Art möglich sind, dann ist es möglich eine Schnittmenge \(W\) finden, die nicht leer ist. Algebraisch ausgedrückt in: \(x_{\alpha}:(U_{\alpha}) \rightarrow S\) and \(x_{\beta}:(U_{\beta}) \rightarrow S\) haben die Relation \(x_{\alpha}(U_{\alpha}) \subset x_{\beta}(U_{\beta}) = W = \not0\). Zuordnungen(Funktionen) obiger Art, die irgendwie verkettet, bzw. verknüpft sind, sind dann differenzierbar und es kann von einer differenzierbaren Mannigfaltigkeit gesprochen werden. \(x^{-1}_{\beta} \circ x_{\alpha}:x_{\alpha}^{-1}(W) \rightarrow R^{2}\) und \(x_{\alpha}^{-1}\circ x_{\beta}:x_{\beta}^{-1}(W) \rightarrow R^{2}\)
Höher dimensionale Mannigfaltigkeit #
Eine differenzierbare Abbildung höheren Grades wird mit ihrer Nachbarschaft in folgender Abbildung dargestellt:
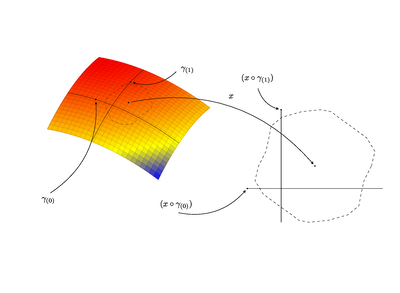
Wie in obiger Abbilung zu erkennen, lassen sich im Prinizp auch nahe Punkte als Nachbarschaft wählen, die entsprechend differenzier- bzw. unterscheidbar ist. Statt nur eine Dimension zu beachten, können hier Änderungen in 2 Dimensionen beobachtet werden. Würden wir eine weitere Koordinate einführen, an der Änderungen gemessen werden, ist die Differzenierung in 3 Dimensionen möglich. Allerdings verändert sich im Bereich einer Nachbarschaft die Steigung kaum merklich. D.h. es könnte uns dort erlaubt sein mit einfachen Rechenoperationen, wie Differenzen, Teilern o. ä. zu rechnen, bevor komplizierte Ausdrücke wie verkettete Funktionen in Betracht gezogen werden müssen
Die Grafiken sind im übrigen nicht von mir, sondern unter folgenden Adressen im Netz zu finden: